Learning Goal
This tutorial will introduce you to the basics of Causal Loop Diagrams, and provide you with some examples to help you get started with modeling your own complex systems.
Scope
After completing this introductory tutorial, you will be able to:
- Read and interpret a Causal Loop Diagram
- Understand the basic concepts behind modeling complex systems
- Be able to create your own Causal Loop Diagrams
Structure
This tutorial is structured in three main sections:
| Section | Learning Goal | Duration |
|---|---|---|
| Basic Concepts | Understand what elements, and relationships between elements signify. | 10' |
| Feedback Loops | Understand the different types of feedback loops. | 5' |
| Real-world Examples | Interpret and create Causal Loop Diagrams. | 5' |
Introduction
Systems Thinking is an approach to understanding and solving complex problems by viewing them as parts of an interconnected whole rather than in isolation. It involves recognizing patterns, relationships, and feedback loops within systems to better anticipate the impact of decisions and actions, thereby enabling more holistic and effective solutions.
In order to model these complex systems, we use a variety of tools and techniques to help us visualize and understand the relationships between
various elements within our chosen system. One such tool is the Causal Loop Diagram, which is a graphical representation of the feedback loops
that (likely) exist within a system.
Basic Concepts
The basic building blocks of a Causal Loop Diagram are Nodes and Links. Nodes represent the elements within the system that we are modeling.
These are concepts, objects, or entities that interact with each other in some way. They are generally depicted as circles, boxes, or words, and
are written down as nouns or noun phrases.
Links represent the relationships between the nodes. These are the connections, influences, or dependencies that exist between the elements of the diagram. They are generally depicted as directed arrows or simple lines. The direction of the arrow indicates the nature of the relationship. A node can either have no effect, a strengthening effect, or a weakening effect on the node it connects to. In other words, if the quantity of one node increases, what happens to the quantity of the other node?
- Same: If the quantity of one node increases, the quantity of the other node also increases.
This is depicted by a line with an arrowhead (and optionally a+orSsign). Mathematically, this is know as a correlation. - Opposite: If the quantity of one node increases, the quantity of the other node decreases.
This is depicted by a line with an arrowhead and a−orOsign. Mathematically, this is known as an inverse correlation. - None: If the quantity of one node increases, the quantity of the other node remains the same. This is the easiest to draw, as you don’t need to draw any line at all.
Chickens and Eggs
To illustrate these concepts, let’s consider the classic example of chickens and eggs. In this system, we have two nodes: number of chickens
and number of eggs.
The relationship between these two nodes is that chickens lay eggs, and eggs hatch into chickens. This creates a reinforcing loop, as
the amount of chickens increases the amount of eggs, which in turn increases the amount of chickens.
This gives us a causal loop diagram that looks like this:
Chickens and Roads
Now let’s consider another aspect chickens are known for: crossing roads.
In this system, we have two other nodes: number of chickens, and number of road crossings.
As any chicken owner will tell you, the more chickens you have, the more likely they are to cross the road.
So, as the amount of chickens increases, the amount of road crossings also increases.
And as any road safety officer will tell you, the more road crossings you have, the more likely you are to have chickens being run over.
Hence: as the amount of road crossing increases, the amount of chickens decreases.
Chickens, Eggs, and Roads
Now, let’s combine these two systems into one big system. We end up with our three nodes: number of chickens, number of eggs, and number of road crossings. Note that there is no direct relationship between eggs and road crossings, so we don’t need to draw a link between them.
This gives us a causal loop diagram that looks like this:
We have now created a simple causal loop diagram that shows the relationships between chickens, eggs, and road crossings. This diagram helps us reason about the system and understand how changes in one element can affect the others. As we add more nodes and links to the diagram, we can model more complex systems and explore the feedback loops that exist within them.
We could now start asking questions like: “What happens if we introduce a new road safety measure that reduces the number of road crossings?” or “If we increase the number of chickens, how will that affect the lives of our neighbours?”.
This is just the beginning of what you can do with causal loop diagrams. In the next section, we will explore some more advanced concepts. These will help you create more detailed and accurate models of complex systems if so desired.
Feedback Loops
A key concept in systems thinking is the idea of feedback loops.
Feedback loops are the mechanisms through which changes in one part of a system are amplified or dampened by the system itself.
It is important to understand the different types of feedback loops, as they can have a significant impact on the behavior of a system.
Reinforcing Feedback
Consider our “chickens and eggs” example.
The relationship between the elements chickens and eggs is an example of a reinforcing feedback loop.
Meaning that an increase in one element leads to an increase in the other, which in turn leads to a further increase in the first element.
Note that as the relationship is identical, a decrease in one element will lead to a decrease in the other.
This type of feedback loop can lead to exponential growth or decline in a system.
In some depictions, this type of feedback loop is indicated by an ‘R’ character with a loop around it. Reinforcing feedback loops
are also called positive feedback loops sometimes.
Balancing Feedback
In our “chickens and roads” example, the amount of ‘road crossings’ evolves similarly to the amount of ‘chickens’.
This means that as the number of ‘chickens’ increases, the number of ‘road crossings’ increases as well.
And when the number of ‘children’ decreases, the number of ‘road crossings’ decreases as well.
Many of those chickens will be run over, which will decrease the number of chickens. So as the amount of road crossings increases, the amount
of chickens decreases, which in turn decreases the amount of road crossings.
This is a prime example of a “balancing feedback loop”. A balancing feedback loop is a stabilizing mechanism that tends to keep a system in some sort of equilibrium (a fancy word for “balance”). As time goes on, the system will tend to stabilize itself around a certain value. In nature, this is often referred to as the “homeostasis” of an ecosystem. Think about the predator-prey relationship between wolves and deer. As the number of wolves increases, they eat more deer, which decreases the number of deer. The wolves then have less to eat, so their numbers start dwindling. This in turn allows the deer population to recover, and the cycle starts anew.
This type of feedback loop can lead to oscillations around a certain value. Even if the system is never truly in an equilibrium, it will average out around it
In some depictions, this type of feedback loop is indicated by a ‘B’ character with a loop around it.
Balancing feedback loops are also called negative feedback loops sometimes.
Real-world Examples
Below are some real-world examples of causal loop diagrams. These diagrams are used to model complex systems and understand the relationships between various elements within them. They can help us identify the feedback loops that exist within the system and predict how seemingly small, local, changes can have far-reaching consequences.
Electrical Mini-Grids
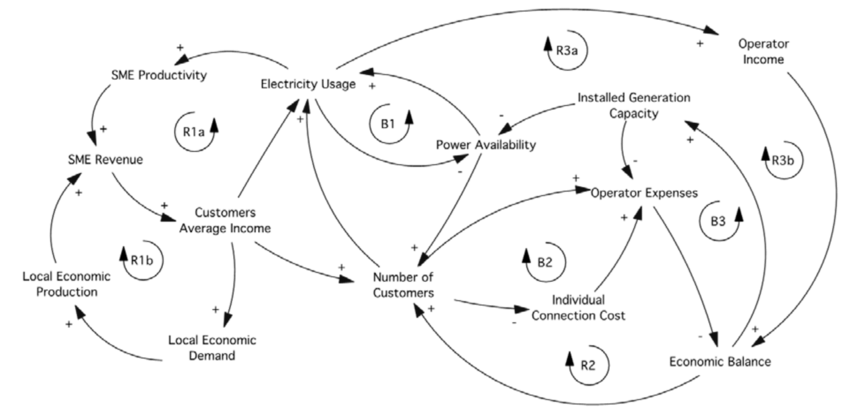
The diagram below illustrates the economical impact of using electrical mini-grids to counter challenges with centralized electrical facilities. Most notably, they are seen as a way to provide electricity to remote areas that are not connected to the main grid. They can also be used to ensure a more stable local supply of electricity, to reduce the risk of full-scale blackouts and ensure a more stable supply of electrical power. If you are interested in the full research paper, you can find it on the Research Gate website.
The included diagram shows the relationships between the different elements of the system. The diagram is used to illustrate the economical impact of introducing electrical mini-grids in rural India. We can identify several feedback loops in the diagram, such as the reinforcing loop on the “local economical demand”. And we can easily spot the balancing feedback loop between “Electricity usage” and “Power availability”.
tip:To grasp the full complexity of systems, such as this one, try and figure out what happens when you change the value of a single element in the diagram. For example, what happens if the “local economical demand” increases? Or what happens if the “power availability” decreases?
Follow the arrows (trace them with your finger or a pen) and see how the changes propagate through the system. More often than not, you will have touched upon nearly all elements in the diagram and usually end up back at the starting point. You will have a better understanding of the modelled system interactions and the impact a single change can have. You might also end up with a slight headache.